進捗報告 その1
以前紹介した「方策勾配を用いた教師有り学習によるコンピュータ大貧民の方策関数の学習とモンテカルロシミュレーションへの利用」
を実装したい、と臨んだ私だったが、
プログラミング能力も足らず要領も悪く、なかなか遅々として進まない。
というところで進捗報告を書きたい。
この実装をするにあたっての手順は次の通り。
1. uecda_serverを使って棋譜を採取
2. 棋譜を学習する特徴要素に変換。局面ごとに提出した手と提出しなかった手の組を作っていきテキストとしてファイル出力。
3. 2のテキストをいったん読み込み、各特徴要素ごとの分散の値を計算して保存。
4. 2と3のテキストを読みながら学習。終わったら重みベクトルを保存。
5. 4のファイルをクライアントで読み込み、対戦。
論文中に使用されている特徴要素は多々あるが、
とりあえず試しにsnowlの3パターンわけだけ実装してやってみた。
ちなみに革命中の学習ものぞいているのでここでやっているのは
「通常時で、3人以上でプレイしていて、必勝手のないとき」
の局面についてだけである。
さらに学習に使用した試合数は10000試合のみ。
(これは何度かやったが40000試合やっても大して値に変化がなかったから。学習係数をうまく調整すればうまくいくのかどうなのか)
標準クライアントでやってみると、こんな感じである。
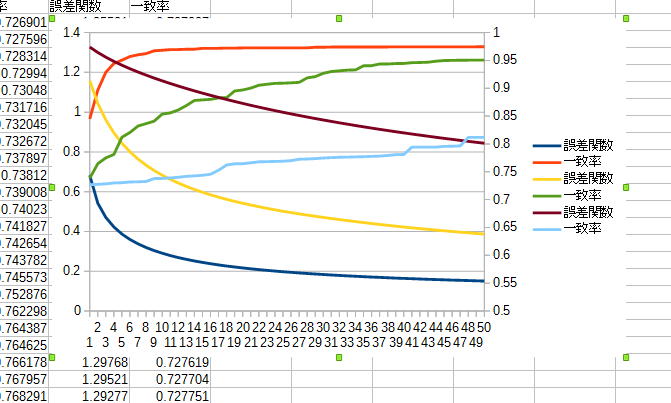
なんとも見づらい、見やすくする配慮を全くしていないのだが、まあ気にしない。
左がテストデータに対する誤差関数の一局面あたり平均で、右が一致率。
3組もあるのは学習係数を論文の0.00005と、その1/10、さらに1/10を試しているからで、ある。
これで対デフォルト対戦をやってみると10000試合で
0.00005のとき28379 (デフォルト 30081 30502 30550 30488)
0.000005のとき28551 (デフォルト 30090 30506 30401 30452)
0.0000005のとき27760 (デフォルト 30487 30321 30853 30579)
一致率を見ると9割5分くらいは的中できているようだが、
強さを見てみるとデフォルトよりも若干下回る。
だが、とりあえず、学習はうまくいっている、と見ていいのだろうか・・・?
論文の通りであるならば、強いクライアントを教師にすれば、強い重みベクトルをゲットできるはず!
期待を胸に11回優勝クライアントGlicineから棋譜を採取し、早速学習に…。
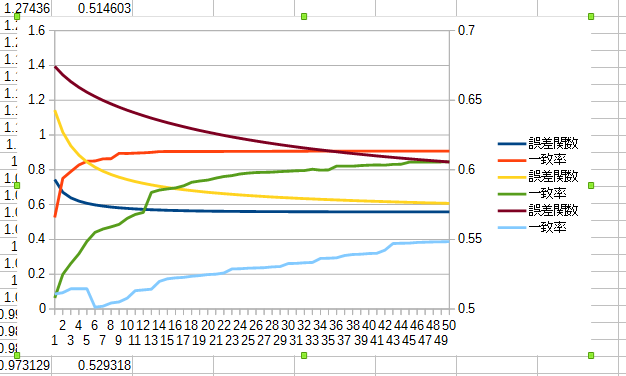
一致率が6割ちょいくらい。まあ、論文でもそれくらいだし大丈夫でしょ。
対戦させてみると
26788 (デフォルト30474 30570 31080 31088
25833 (デフォルト30753 30929 31624 30861
21987 (デフォルト31704 32028 32079 32202
…って、弱くなってるやないかーい!
と、まあこういうことを、最近、というか結構長いことやっているわけです。
(なんども怪しいところは見直したし、もうバグはないと信じたいけど…、まあどっかにあるんだろうけど)
ちなみにkou2でも試したのですが同じようにデフォルトから学習したものよりも弱かったです。
ただ、特徴要素を増やした結果、かすかな希望が生まれました。
31229 (デフォルト29617 29502 29649 30003)
特徴要素を増やしても減らしても、一致率自体には大して変動はないのですが、
なんだかちょっと強くなっていました。
この差が一体なんなのか、よくわかっていませんが。
それにしても、対デフォルト比で大して強くなっていないのは、なんかおかしいのかなあ、です。
学習は愚直に論文中の勾配を計算して更新して、というのをc++で書いておるので、
サーバも自前、学習も自前、対戦も自前、と
プログラミング苦手なのになんでそんなバグの危険しかない道を通っているんだと、我ながら思うのですが。
もっと学習の知られざるテクニックがあるのか、
もっとミソの詰まった特徴要素があるのか、(あるいはそこにバグがあるのか)
なんだかもうわけが分からないです。
また悩みをぶちまけるかもしれないですが、
その時は少しは進捗があるといいね。
ちなみに勾配降下法っていうけど、
「W-KEYAKIZAKAの詩」にこういう詩があるんだ。
「平坦だと信じていた目の前の道、ほんの少し傾斜してる、それは希望かもしれない」
「明日に続くこの角度、上り続けていく」
誤差関数だけど、マイナスをかけないで、プラスに駆け上がっていくイメージで攻めていかないか。
おじさん、この曲好きなんです。