2017-05-09

進捗報告その３

大貧民

前回の記事で

理想とすれば、もう少し緩やかな傾斜を描いて、一致率を向上させていく、というのがよさそうな感じはある。もう少し学習率の微調整を試すべきであろうか。

と書いたので、これの続きです。

学習率を小さくとって、少しずつ動かしていきます。

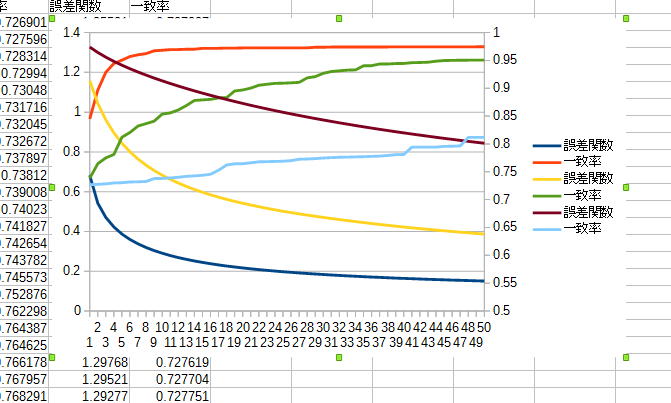
まず0.0000005で挑戦。これまでは50回しか学習を繰り返していませんでしたが、 100回まで試してみました。結果がこちら。

テストデータに対する誤差関数の値は、確かに下がっています。 f:id:koganie:20170508225343p:plain

ただ学習結果で対戦させてみると、こんな感じ。 f:id:koganie:20170508224703p:plain

・・・ん？

f:id:koganie:20170508233455p:plain

ネコかなあ！？

40をピークにして、あとは平均得点は下がっている。誤差関数は下がっているのに、である。

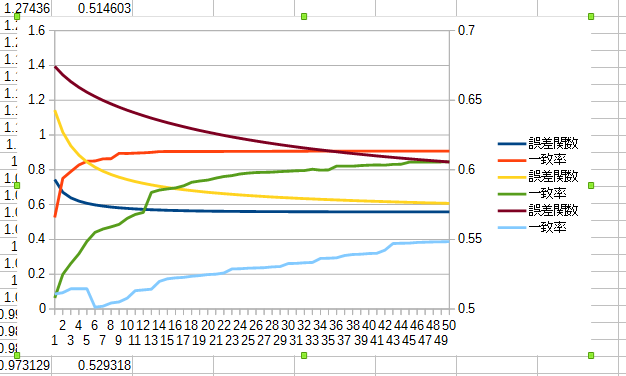
次に0.0000001で挑戦。こちらはさらに小さいので150回やっており、順調に下がっています。 f:id:koganie:20170508230647p:plain

対戦の結果はこちら。 f:id:koganie:20170509231910p:plain こちらは若干右肩上がりに見えるが、3.2前後のところで上げどまっている。

これまであまりに「誤差関数は下がっているのに対戦成績に反映されないのはおかしい」という点にこだわってきたが、さすがに受け入れなくてはいけない。つまり、これまであまりに直視してこなかったけど、「特徴要素」をもっとうまく設定すれば、強さに反映されるんでは？いまの特徴要素ではどうあがいてもこれくらいが限度ってことなんでは？

ともかく、学習自体はうまくいっているように見える。今度は特徴要素に注意して実験を行ってみようぞ。

2017-05-01

進捗報告その２

大貧民

前回の、コンピュータ大貧民挑戦の続き。
進捗報告その１ - koganie’s blog

前回、特徴要素を増やし、kou2相手に学習したところ、
対デフォルトでようやく勝ち越すことができました。
学習の仕方を変えてみたらもっと強くなるでしょうか？

学習率0.00005で10000試合分学習して、10000試合対デフォルトで対戦した結果
31151 29734 29515 29740 29860（得点。一番左が学習クライアント、それ以外はデフォルト）
で、デフォルトよりは若干強くなっているようです。
では、このまま40000試合分学習させてみましょう…の結果がこちら。
31013 29665 29806 29703 29813
見事に弱くなっています。
学習の際に、学習率に対し0.999を毎回かけて減衰させていった結果がこちら。
31169 29843 29432 29975 29581
f:id:koganie:20170430235703p:plain

続いて学習率を1/10して同じようにした結果。
32772 29519 29182 28990 29537
さっきより強くなっている！
では学習データを増やせば…！
31671 29645 29672 29268 29744
弱くなっている！なんでだ！
上では減衰させたが、こちらでは論文にもあるL2正則化を試してみる。

L2正則化というのは、誤差関数に
$R(w)=\lambda ||w||^2_2$
を足したもの（ $\lambda$ は正則化項の学習係数）。
$||w||_p=\sqrt[p]{|w_1|^p+...+|w_n|^p}$
をp-ノルムというようで、
ノルム - Wikipedia
すなわち
$\frac{\partial \lambda R(w)}{\partial w}=2\lambda w$
正則化 - Wikipedia
を、勾配に足していくというもの。（たぶん）

で、学習した結果がこちら。
31722 29152 29818 29986 29322
あってもなくても、大して効果はないようだ…。

f:id:koganie:20170501000623p:plain

どちらにせよ、テストデータに大して誤差、一致率とも向上はしているので
「過学習」をしているとは言いづらい。
実際、一致率は若干ではあるが、データ数多いほうが大きな数値をとっている。
が、現実問題としてデータ数を増やすと弱くなってしまうというのは、
過度に学習をしてしまっている、ということなのだろうか？

理想とすれば、もう少し緩やかな傾斜を描いて、
一致率を向上させていく、というのがよさそうな感じはある。
もう少し学習率の微調整を試すべきであろうか。

なんだかやる気がおきない。
もっとこう、劇的な変化してほしいが。果たして。

2017-04-24

進捗報告その１

大貧民

以前紹介した「方策勾配を用いた教師有り学習によるコンピュータ大貧民の方策関数の学習とモンテカルロシミュレーションへの利用」
を実装したい、と臨んだ私だったが、
プログラミング能力も足らず要領も悪く、なかなか遅々として進まない。
というところで進捗報告を書きたい。

この実装をするにあたっての手順は次の通り。
1. uecda_serverを使って棋譜を採取
2. 棋譜を学習する特徴要素に変換。局面ごとに提出した手と提出しなかった手の組を作っていきテキストとしてファイル出力。
3. 2のテキストをいったん読み込み、各特徴要素ごとの分散の値を計算して保存。
4. 2と3のテキストを読みながら学習。終わったら重みベクトルを保存。
5. 4のファイルをクライアントで読み込み、対戦。

論文中に使用されている特徴要素は多々あるが、
とりあえず試しにsnowlの3パターンわけだけ実装してやってみた。
ちなみに革命中の学習ものぞいているのでここでやっているのは
「通常時で、３人以上でプレイしていて、必勝手のないとき」
の局面についてだけである。
さらに学習に使用した試合数は10000試合のみ。
（これは何度かやったが40000試合やっても大して値に変化がなかったから。学習係数をうまく調整すればうまくいくのかどうなのか）

標準クライアントでやってみると、こんな感じである。
f:id:koganie:20170423235140p:plain
なんとも見づらい、見やすくする配慮を全くしていないのだが、まあ気にしない。
左がテストデータに対する誤差関数の一局面あたり平均で、右が一致率。
３組もあるのは学習係数を論文の0.00005と、その1/10、さらに1/10を試しているからで、ある。

これで対デフォルト対戦をやってみると10000試合で
0.00005のとき28379 （デフォルト　30081 30502 30550 30488）
0.000005のとき28551 （デフォルト　30090 30506 30401 30452）
0.0000005のとき27760 （デフォルト　30487 30321 30853 30579）

一致率を見ると９割５分くらいは的中できているようだが、
強さを見てみるとデフォルトよりも若干下回る。
だが、とりあえず、学習はうまくいっている、と見ていいのだろうか・・・？

論文の通りであるならば、強いクライアントを教師にすれば、強い重みベクトルをゲットできるはず！
期待を胸に11回優勝クライアントGlicineから棋譜を採取し、早速学習に…。

f:id:koganie:20170424000925p:plain

一致率が６割ちょいくらい。まあ、論文でもそれくらいだし大丈夫でしょ。
対戦させてみると
26788 （デフォルト30474 30570 31080 31088
25833 （デフォルト30753 30929 31624 30861
21987 （デフォルト31704 32028 32079 32202

…って、弱くなってるやないかーい！

と、まあこういうことを、最近、というか結構長いことやっているわけです。
（なんども怪しいところは見直したし、もうバグはないと信じたいけど…、まあどっかにあるんだろうけど）

ちなみにkou2でも試したのですが同じようにデフォルトから学習したものよりも弱かったです。
ただ、特徴要素を増やした結果、かすかな希望が生まれました。
31229 （デフォルト29617 29502 29649 30003）
特徴要素を増やしても減らしても、一致率自体には大して変動はないのですが、
なんだかちょっと強くなっていました。
この差が一体なんなのか、よくわかっていませんが。
それにしても、対デフォルト比で大して強くなっていないのは、なんかおかしいのかなあ、です。

学習は愚直に論文中の勾配を計算して更新して、というのをc++で書いておるので、
サーバも自前、学習も自前、対戦も自前、と
プログラミング苦手なのになんでそんなバグの危険しかない道を通っているんだと、我ながら思うのですが。

もっと学習の知られざるテクニックがあるのか、
もっとミソの詰まった特徴要素があるのか、（あるいはそこにバグがあるのか）
なんだかもうわけが分からないです。

また悩みをぶちまけるかもしれないですが、
その時は少しは進捗があるといいね。

ちなみに勾配降下法っていうけど、
「W-KEYAKIZAKAの詩」にこういう詩があるんだ。
「平坦だと信じていた目の前の道、ほんの少し傾斜してる、それは希望かもしれない」
「明日に続くこの角度、上り続けていく」

誤差関数だけど、マイナスをかけないで、プラスに駆け上がっていくイメージで攻めていかないか。

youtu.be

おじさん、この曲好きなんです。

2017-04-15

日記　けやき坂

日記

けやきの「誰よりも高く跳べ」はMVでぴょんぴょん跳ねててかわいかった。シンプルにダンスに焦点を当てていてとてもよかった。

今回の「僕たちは付き合っている」もいい曲で、ダンスもかわいいのだけど（くそかわいくない？）、 MVはよくわからないドラマ仕立てがメイン。前みたいにシンプルでよかったのになあ、と思うのです。

しかし本当、このドラマは何をやっているんだろう。意味が分からない。

2017-04-11

交流③

電気の勉強

前回のがRLC直列回路のインピーダンスで、
同じような感じに並列回路のインピーダンスも考えることができる。

直列のインピーダンスが
$\dot{Z}=R+jX_L+\frac{1}{jX_C}$
だったように、並列のインピーダンスは
$\frac{1}{\dot{Z}}=\frac{1}{R}+\frac{1}{jX_L}+jX_C=\frac{1}{R}+j(X_C-\frac{1}{X_L})$

で、これの逆数をとればいいわけだが、面倒くさいのでやらない。

実はインピーダンスの逆数を、アドミタンスといって、計算をよく簡略化するようである。
$\dot{Y}=G+jB$
実数部のGをコンダクタンス、虚数部のBをサセプタンスという。単位はジーメンス[S]。
ここにきてアニメの終盤を彷彿とさせる怒涛の用語攻勢である。
ただの逆数だろうに、どうしてこんな紛らわしいことをするのだろう。

上記でいえば
$G=\frac{1}{R}$
$B=X_C-\frac{1}{X_L}$

ここまでくるとようやく交流回路の問題が解けるようになる。
実際にはこの先三相交流というまたよくわからん代物が登場するのだが。

それはまた別のお話である。

2017-04-10

交流②

電気の勉強

コイルのインダクタンスL[H]のとき、自己誘導起電力は次の式。
$e=-L\frac{\Delta I}{\Delta t}$
電流の変化による磁束の変化を妨げるような起電力。
つまり交流電流を流すと、こいつがなにか作用をするということ。

コイルだけの交流回路を考えたとき
$v+e=0$
より
$v=L\frac{\Delta I}{\Delta t}$

$i=\sqrt{2}I\sin{\omega t}$
を代入すれば、 $t$ で微分して
$v=\sqrt{2}I\omega L\cos{\omega t}$
ということで、電流は電圧より位相が遅れる。

$v$ の実効値 $V$ とすると
$\frac{V}{I}=\omega L$
オームの法則でいう抵抗にあたるものだが、交流におけるコイル・コンデンサに対するこれをリアクタンスという。
$X_L=\omega L$

一方、静電容量 $C$ のコンデンサについても、同じように考えることができて、
$Q=CV_C$
とキルヒホッフの第二法則でコイルと同じように
$v=\frac{Q}{C}$
という式が作れる。
ここで電流は
$i=\frac{\Delta Q}{\Delta t}$
で表されるので、上式と合わせて微分すると
$i=\frac{\Delta Cv}{\Delta t}=\frac{\Delta \sqrt{2}CV\sin{\omega t}}{\Delta t}=\sqrt{2}\omega CV\cos{\omega t}$
ということで、こちらは電流は電圧よし位相が進む。

同じように実効値を見ると
$\frac{V}{I}=\frac{1}{\omega C}$
なので、コンデンサのリアクタンスは
$X_C=\frac{1}{\omega C}$

では抵抗 $R$ と、コイル、コンデンサが直列につながった回路はどうなるか。
こう、リアクタンスと抵抗とを一緒に考えた抵抗値を、インピーダンスという。
微妙な意味合いの違い、言葉の違い、ややこしい。
$\dot{Z}=R+jX=R+j(X_L-X_C)$
抵抗は実数部、リアクタンスは虚数部を使って表現する。
ベクトル表示においてjを書けることは $\pi/2$ 進め、-j書けることは遅らせることと対応させることができる、ということらしい。